This Post Has 7 Comments

  1. How did you do on #15, #21, #22, #30, #31…..?
    Too many good ones to mention in this problem set. It’s a good one to show how the problem sets are focused on testing your ability to unwrap shorter math puzzles and how well you know your definitions. If you’re not methodical and paying close attention then a lot of unwanted mistakes will result. We definitely want you to avoid that on the real exam.

    1. #37
      If the area of the one circle is 16pi then we can determine the radius of that circle.
      AREA(circle )= Pi x Radius Squared
      16 x Pi = Pi x Radius Squared
      …so the radius squared equals 16. The radius of the circle is the square root of 16 as a result so the radius of circle one is 4.
      If that radius of circle one, 4, is the diameter of the second circle…
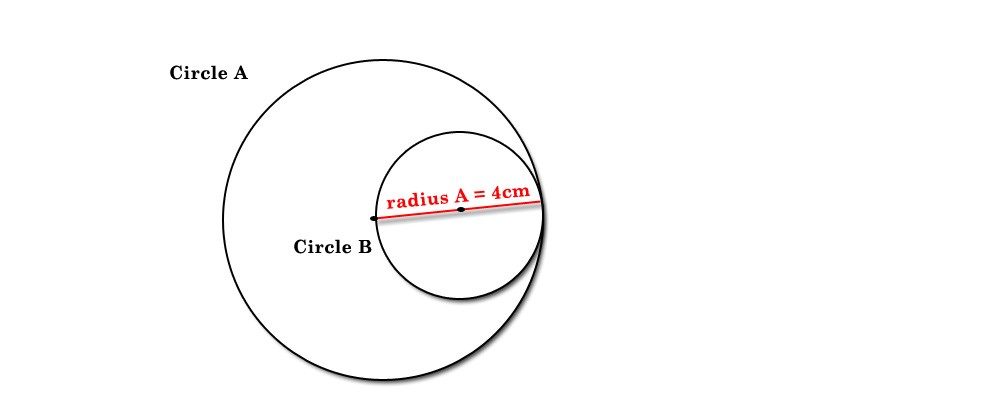
      Circle Overlapping
      then the radius of the second circle must be 2 (half the diameter). The center point of each circle is separated by the radius of the second circle as shown in the picture above. That means the center points of the circles are 2 units apart.

      2. Thank you for your help! The reason I was confused was because there was a typo on both of those questions. It seems that you have fixed them!

    2. #38
      If the series sum of 51 + 52 + 53 + 54…+ 99 + 100 = 3,775 then what is the sum of the series 101 + 102 + 103 + 104 + …149 + 150 = ?
      At the risk of repeating the written answer explanation, I will point out that each term in the second series is +50 more than the corresponding term in the first series. Note 101 is 50 more than 51. 102 is 50 more than 52. 103 is 50 more than 53 and so on to the last term 150 which is +50 more than 100. In all that is 50 terms.

      As a result,
      SUM SERIES(2) = SUM SERIES(1) + 50 terms x 50 difference for each term
      SUM SERIES(2) = 3,775 + 50×50 = 3,775 + 2,500 = 6,275

      I hope that helps clarify the answer. If not there is another approach, but noticing the +50 difference for every term is probably the easiest way to get to the answer and find the new sum.

Leave a Reply

This site uses Akismet to reduce spam. Learn how your comment data is processed.

Back To Top